Smart street light using arduino
- Atmega 8a (based on arduino ng board)
- 8 high-intensity led
- Relay
- Perfboard
- 7805
- connecting wires
- solar panel (9 volt, 2.5 watt)
- Relay
- 12 volt DC motor.
| DIY IR sensor |
Check out the video:
| DIY IR sensor |

Connor Nishijima has devised a neat trick to give the standard Arduino Tone() function 256 smooth volume levels using PWM at an ultrasonic frequency, without any extra components. This allows for programmatic control of square waves with nothing other than a speaker connected to an Arduino Uno.
Normally to simulate an analog voltage with a digital-only pin of a microcontroller you’d use Pulse Width Modulation. This works great for LEDs because your eyes can’t the 490 / 976Hz flicker of the standard analogWrite() function. But for audio things are a bit more difficult. Because your ears can easily detect frequencies between 20 – 20,000Hz, any PWM with a frequency in this range is out.
Luckily, the ATmega328P allows you to change the clock prescalers for ultrasonic PWM! We need to use Timer0, because it can drive PWM at a max frequency of 62,500Hz, which even if you cut that in half would still be above your hearing range. Now that we have ultrasonic PWM on Pins 5 & 6, we configure Timer1 to fire an Interrupt Service Routine at a rate of “desired frequency” * 2.
Finally, inside the Timer1 ISR routine, we incorporate our volume trick. Instead of digitalWrite()’ing the pin HIGH and LOW like the normal Tone() function does, we analogWrite() “HIGH” with our volume value (0 – 255) and analogWrite(0) for “LOW”. Because of how fast the PWM is running, the user doesn’t hear the 62.5KHz PWM frequency, and instead perceives a 50% percent duty cycle as a speaker driven with only 2.5 volts! While a few volume levels do produce subtle artifacts to the sound, it mostly delivers quality 8-bit volume control to replace the standard Tone() function.
When all is said and done, you’ll be able to customize your project with unique loudness as you play anything from the iconic Nintendo sound to R2-D2’s beeps and bops. In Nishijima’s case, he developed this Arduino volume-control scheme to make an incessant, inconsistent artificial cricket to hide in a friend’s vent for the next few months… You can read more on its Hackaday.io page, as well as find documentation and ready-to-use example sketches GitHub.
| Schematic of temperature controlled fan |


1 | /* ================================================================================================================================================== |
1 | /* ================================================================================================================================================== |



However, if you do not have a google profile...
Feel free to share this page with your friends in any way you see fit.


1 | /* ================================================================================================================================================== |
1 | /* ================================================================================================================================================== |



However, if you do not have a google profile...
Feel free to share this page with your friends in any way you see fit.
Classes start tomorrow, so I spent yesterday making sure that the incubator control project was feasible. I had gotten the fan feedback control working well back in September, but I’d put the project aside for Fall quarter and only got back to it this week. As a reminder, here are the previous posts on the project:

Here is the interior of the styrofoam box, with the lid open. The 6″×12″ aluminum plate covers the bottom. The thermistor is on the left, propped up by a rubber foot, the resistor in is the center, and the fan is sitting on a foam pad on the right. (The foam is to reduce noise until I can get the fan proper mounted in a baffle.)
I left the foam out this time, which made for a somewhat noisy fan, and I still haven’t built a baffle—I’m still using the bent-wire-and-paper deflector shown in the photo. What I worked on yesterday was the software—since the temperature changes are fairly slow, it takes a long time to tune the control loops.
One thing I did was to try to reduce measurement noise further on the thermistor measurements. I now add 60 analog-to-digital readings. They’re 10 bits on the Arduino-compatible board (a Sparkfun redboard), so adding 60 still fits in an unsigned 16-bit word. I now get noise of about ±0.05°C, which is half the least-significant-bit of the converter. I doubt that I can do better in precision without switching to a processor with a better analog-to-digital converter, though I could do digital filtering with a 1Hz low-pass filter to smooth out the remaining noise.
I copied the fan feedback control loop (with the anti-windup provisions) described in Improving feedback for fan for temperature control, but made two changes:
Here are some results from tuning experiments:
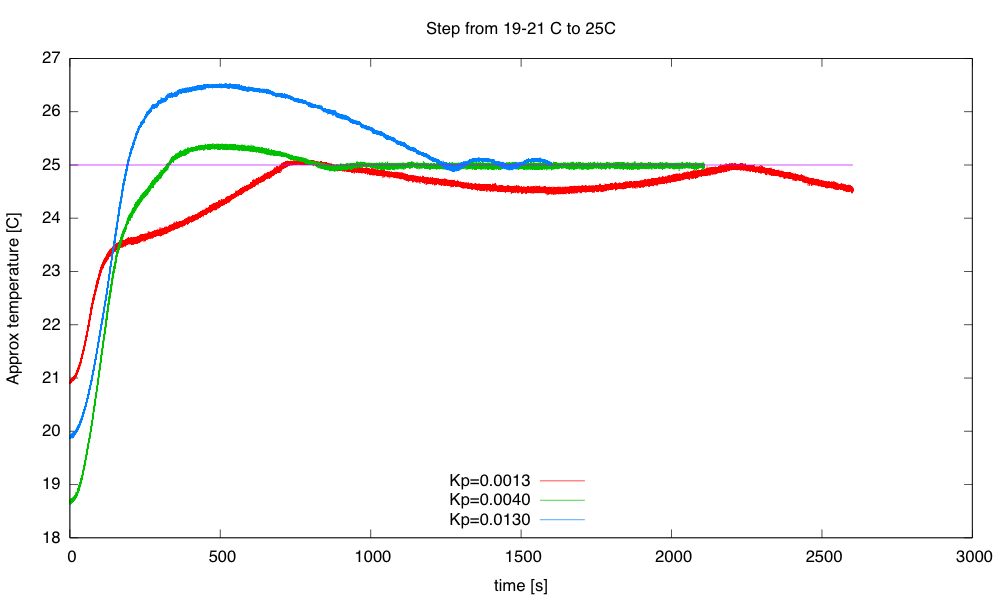
The blue curve switched to PI control at 23.5°C, the other two at 22°C. The green curve has pretty tight control over the temperature, but does overshoot a bit.
The initial temperatures were not all identical, because I wasn’t always willing to let everything cool down all the way to room temperature after each tuning run. I could only do about 1 tuning run an hour, which could pose problems for the freshman design seminar, as we don’t have long lab times—only the 70-minute lecture-schedule meeting times.
I continued the best of those runs with another step, up to 35°C, then let it cool down.

The step to 35°C has more ringing than the step to 25°C. I terminated the run before it had finished cooling, because the 32-bit µs timer wrapped around.
The cool-down at the end fits a 0.0069 °C/s line better than it fits an exponential decay to the ambient temperature. If I do fit an exponential decay curve, I get a time constant of around 1975 seconds.
A simple thermal-resistance, thermal-capacity model is not a very good one for predicting how the system will behave, particularly since we’re not measuring the temperature of the large thermal mass (the aluminum plate and power resistor), but of the air, which has a large thermal resistance from the plate. The time constant for the aluminum-air transfer is larger than the time constant for the electricity-aluminum transfer, which is why we get so much overshoot when we turn off the power to the resistor—the aluminum plate has gotten much hotter than the air, and continues to transfer heat to it, even though no more heat is being added to the aluminum.
Still, it is worth seeing what we get if we model the box a simple thermal mass and thermal resistor. The steady-state 35°C seems to need about 9W (PWM of 51/256) and the 25°C 3W (PWM of 17/256) with an ambient temperature of about 19°C, implying that the styrofoam box has a thermal resistance of about 1.9°C/W.
To see what is really going on, I’ll have to heat the box to 35°C, then start the cool down with a reset 32-bit timer.
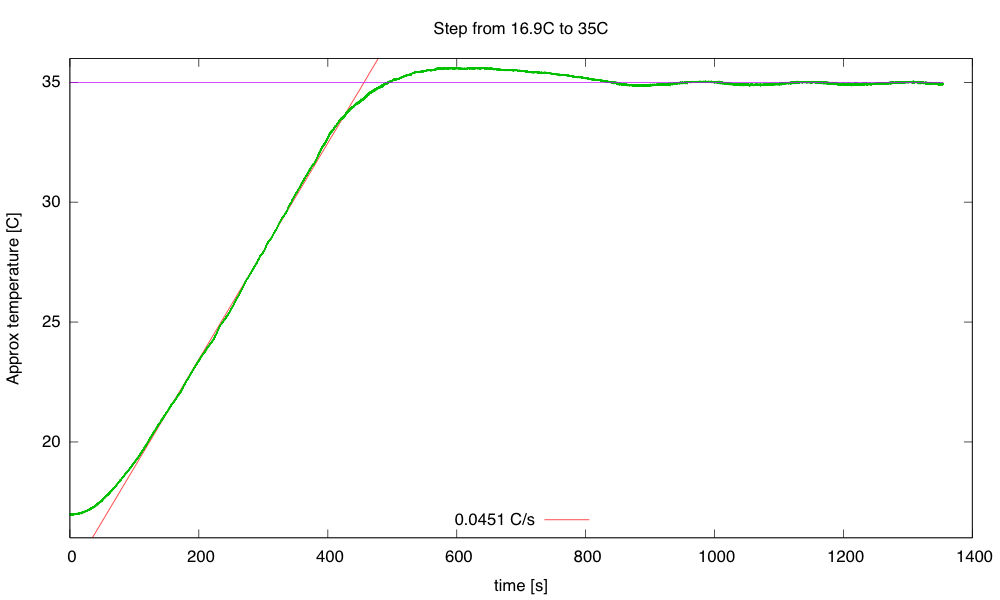
Single-step warming from 16.9°C to 35°C. The steady state at 35°C is about 9.32W, for a thermal resistance of 1.8°C/W. The rise of 0.0451°C/s at 45W implies a thermal capacity of 998 J/°C.
Heating at 45W (9V, 1.8Ω) results in a temperature rise of about 0.0451 °C/s. This warm-up rate at 45W implies a thermal capacity of about 998 J/°C. We may want to adjust our thermal capacity estimate, since some of the 45W put in escapes through the box—maybe about 3–4W at the temperatures where the rise was measured. This reduces the thermal capacity estimate to about 910 J/°C.
The cool down from 35°C starts out as a straight line (about -0.0074°C/s or -26.5°C/hour), but gradually starts behaving more like the exponential we would expect from a thermal-resistance and thermal-capacity model.

The time constant for the cooling is about 1380s, but the initial cooling is too slow for a simple exponential.
The time constant of 1380 s, combined with a thermal capacity of 910 J/°C gives a thermal resistance of 1.5 °C/W, a bit lower than the 1.8°C/W I estimated from the steady-state power.
I continued the cooling (with the timer wrapped around) to see if I got a clean exponential at low temperature differences:

The exponential seems to fit well here, with a time constant of 2300s. Combined with the 910 J/°C, this gives a thermal resistance of 2.5°C/W, which seems a little high compared to the other estimates.
So I’ve made some progress on the thermal control loop (though I’d like to reduce the overshoot and ringing) and I have a crude model for the box: a thermal mass with capacity about 910 J/°C and thermal resistance 2±0.5 °C/W.
Still on my to-do list for this project:
I wanted to look at the step response of the fan and of the heater, so that I could see if I could derive somewhat reasonable control parameters by theory, rather than by cut-and-try parameter fiddling. Most of the tutorials I’ve looked at give empirical ways of tuning PID controllers, rather than theoretical ones, even ones that use Laplace transforms to explain how PID controllers work and how to determine whether or not the control loop is stable if you are controlling a linear time-invariant system with a known transfer function.
When I first looked at the fan response, I noticed a problem with my tachometer code:

The tachometer gives two pulses per revolution, but the markers used are not perfectly spaced, so I get different estimates of the speed depending which falling-edge-to-falling-edge pulse width I measure. The difference between the two speeds is about 1.6%.
I rewrote the tachometer code to trigger on all four edges of a revolution, and to record the time at each edge in a circular buffer. This way I can use a full revolution of the fan for determining the speed, but get updated estimates every quarter revolution, available in micros_per_revolution:
volatile uint32_t old_tach_micros[4]; // time of last pulses of tachometer
// used as a circular buffer
volatile uint8_t prev_tach_index=0; // pointer into circular buffer
volatile uint32_t micros_per_revolution; // most recent pulse period of tachometer
#define MIN_TACH_PULSE (100) // ignore transitions sooner than this many
// microseconds after previous transition
void tachometer_interrupt(void)
{ uint32_t tach_micros = micros();
if (tach_micros-old_tach_micros[prev_tach_index] < MIN_TACH_PULSE) return;
prev_tach_index = (prev_tach_index+1)%4; // increment circular buffer pointer
micros_per_revolution= tach_micros-old_tach_micros[prev_tach_index];
old_tach_micros[prev_tach_index] = tach_micros;
}
In setup(), I need to set up the interrupt with attachInterrupt(FAN_FEEDBACK_INT,tachometer_interrupt, CHANGE);
I think that this improved tachometer code may be a bit too much for first-time programmers to come up with. Circular buffers use a bunch of concepts (arrays, modular arithmetic) and are likely to cause a lot of off-by-one errors. Interrupts alone were a complicated enough concept for students to deal with. I don’t know whether the improvement in speed measurement would be justifiable in the freshman design course.
The new tachometer code did smooth out the measurements a lot, though, as expected—it reduces the fluctuation in measured speed to about 0.3%, which is limited by the resolution of the micros() timer I’m using on the Arduino board. I then tried recording some step responses, both for upward steps and downward steps. The upward steps are reasonably approximated by an exponential decay (like a charging curve):
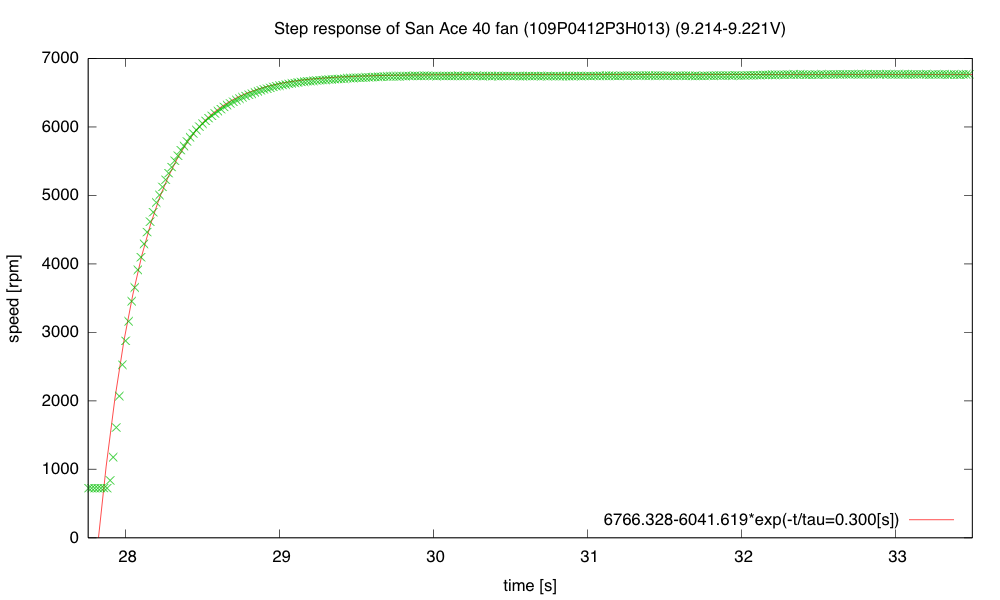
The low speed with PWM=0 (always off) is 724.7 rpm, and the high speed with PWM=255 (always on) is 6766.3rpm. The exponential fit is not perfect, but it is certainly a good enough approximation for designing a closed-loop system.
The response to a downward step, however, is not well modeled by a simple exponential decay:
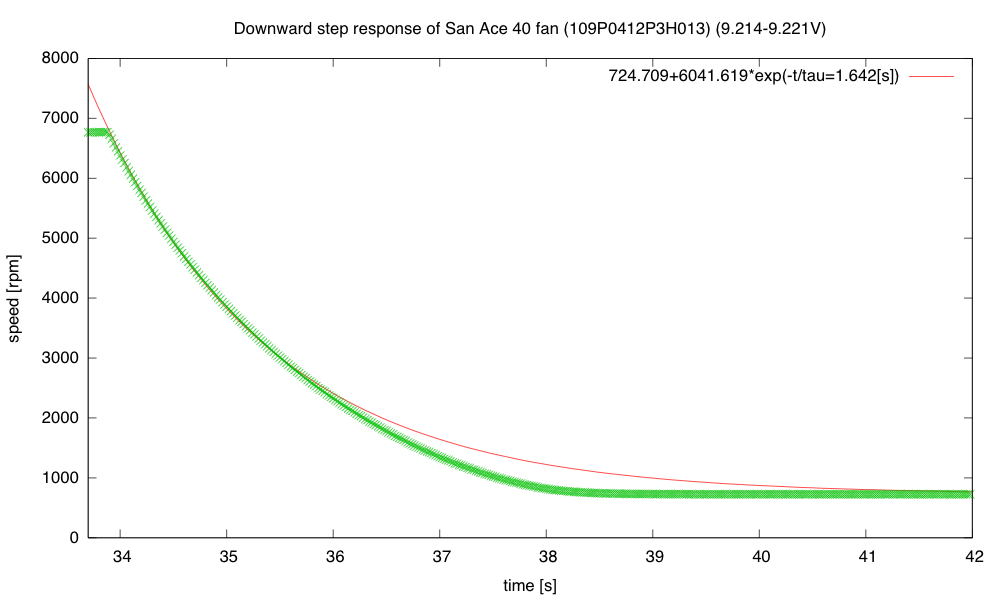
The fan spins down gradually at first (with a time constant about 1.6s), but at low speed the speed changes faster (as if the time constant dropped to about 0.6s).
Note that the fan slows down much more gradually than it speeds up, which means that it is not a linear, time-invariant system. In a linear system, superimposing a step-up and a step-down would cancel, so the responses to the step up and step down should add to a constant value—the fan most definitely does not have that property.
I was curious whether the difference was just apparent for large steps, or also for small ones, so I tried steps between PWM duty cycles of 100/256 and 160/256:
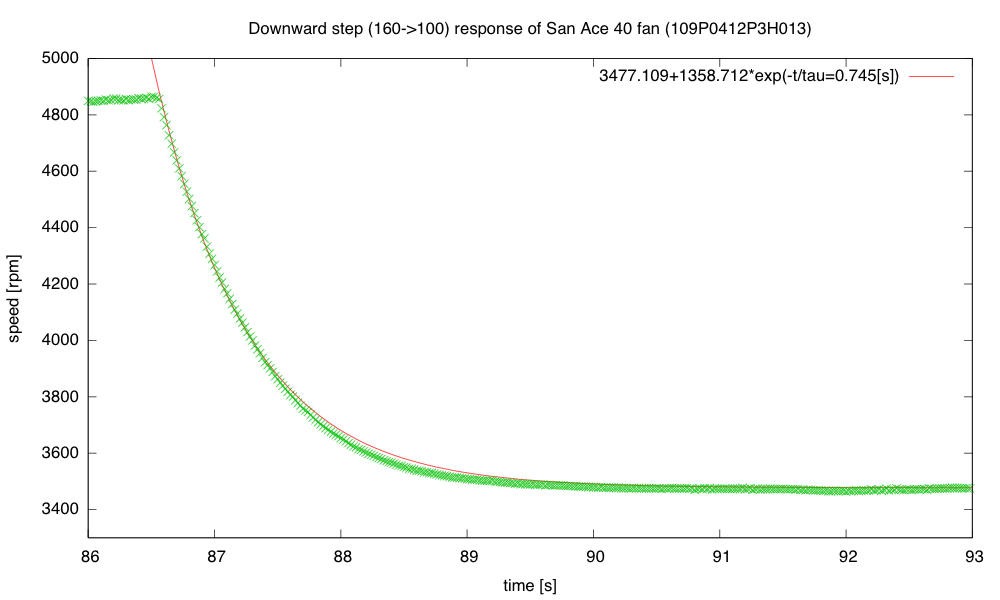
The small downward step is faster than before, though still substantially slower than the upward step of the same size, and with an initially slower response than the final convergence.
I’m going to try writing a couple of ad hoc controllers for the fan, to see if they behave better than the PID controller I’ve been using: open-loop control using just PWM=(setpoint-740)/25; a simple on/off control with a single threshold; hysteresis, using two thresholds instead of 1; PI control with no anti-windup; and a controller that goes to full on or full off when the error is large, to make a quick transition, switching to approximately the right PWM value, when the error is small, with PI control thereafter.
I think that the open-loop controller will have a steady, but wrong speed; the crude on/off controllers will make an audible pulsing of the fan motor; the PI controller will suffer from overshoot when making big steps, and the on/off/PI controller should make nice steps, if I can tune it right.
I implemented all the controllers and ran a test switching between setpoints of 1000RPM and 5000RPM every 30 seconds. Here are plots of the behavior with different control algorithms:

The PWM values computed by the various control algorithms show the integrator windup problem for PI clearly after the downward transitions—PI takes a long time to recover from the errors during the downward edge.
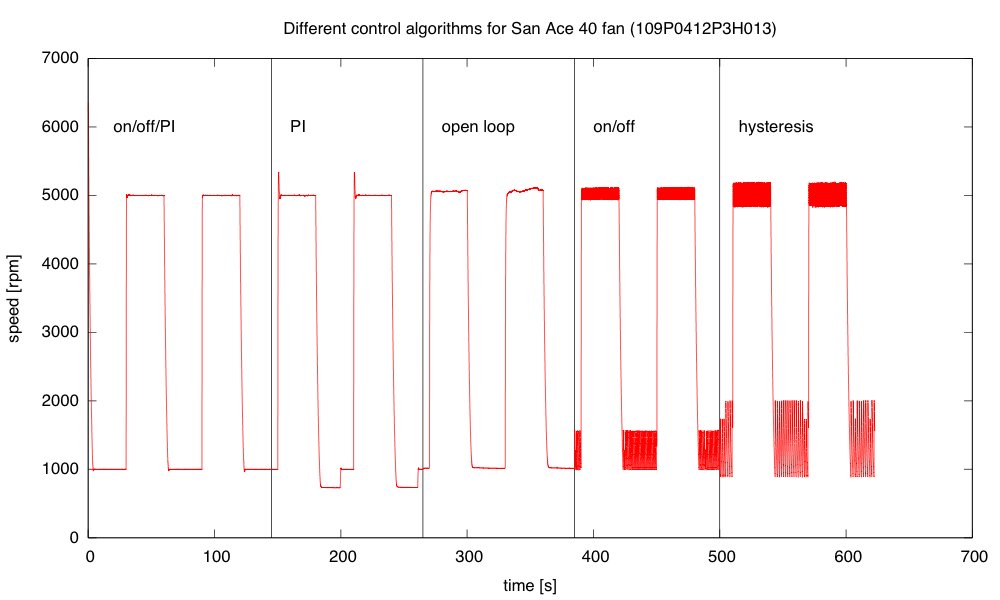
The mixed algorithm does a very good job of control, with little overshoot. The simple PI algorithm has substantial overshoot, particularly when the control loop wants a PWM value outside the range [0,255]. Open loop has significant offset and wanders a bit. On/off control oscillates at about 10hz, and adding hysteresis makes the oscillation larger but slower (about 5Hz).
I wanted to look at the step response of the fan and of the heater, so that I could see if I could derive somewhat reasonable control parameters by theory, rather than by cut-and-try parameter fiddling. Most of the tutorials I’ve looked at give empirical ways of tuning PID controllers, rather than theoretical ones, even ones that use Laplace transforms to explain how PID controllers work and how to determine whether or not the control loop is stable if you are controlling a linear time-invariant system with a known transfer function.
When I first looked at the fan response, I noticed a problem with my tachometer code:

The tachometer gives two pulses per revolution, but the markers used are not perfectly spaced, so I get different estimates of the speed depending which falling-edge-to-falling-edge pulse width I measure. The difference between the two speeds is about 1.6%.
I rewrote the tachometer code to trigger on all four edges of a revolution, and to record the time at each edge in a circular buffer. This way I can use a full revolution of the fan for determining the speed, but get updated estimates every quarter revolution, available in micros_per_revolution:
volatile uint32_t old_tach_micros[4]; // time of last pulses of tachometer
// used as a circular buffer
volatile uint8_t prev_tach_index=0; // pointer into circular buffer
volatile uint32_t micros_per_revolution; // most recent pulse period of tachometer
#define MIN_TACH_PULSE (100) // ignore transitions sooner than this many
// microseconds after previous transition
void tachometer_interrupt(void)
{ uint32_t tach_micros = micros();
if (tach_micros-old_tach_micros[prev_tach_index] < MIN_TACH_PULSE) return;
prev_tach_index = (prev_tach_index+1)%4; // increment circular buffer pointer
micros_per_revolution= tach_micros-old_tach_micros[prev_tach_index];
old_tach_micros[prev_tach_index] = tach_micros;
}
In setup(), I need to set up the interrupt with attachInterrupt(FAN_FEEDBACK_INT,tachometer_interrupt, CHANGE);
I think that this improved tachometer code may be a bit too much for first-time programmers to come up with. Circular buffers use a bunch of concepts (arrays, modular arithmetic) and are likely to cause a lot of off-by-one errors. Interrupts alone were a complicated enough concept for students to deal with. I don’t know whether the improvement in speed measurement would be justifiable in the freshman design course.
The new tachometer code did smooth out the measurements a lot, though, as expected—it reduces the fluctuation in measured speed to about 0.3%, which is limited by the resolution of the micros() timer I’m using on the Arduino board. I then tried recording some step responses, both for upward steps and downward steps. The upward steps are reasonably approximated by an exponential decay (like a charging curve):

The low speed with PWM=0 (always off) is 724.7 rpm, and the high speed with PWM=255 (always on) is 6766.3rpm. The exponential fit is not perfect, but it is certainly a good enough approximation for designing a closed-loop system.
The response to a downward step, however, is not well modeled by a simple exponential decay:

The fan spins down gradually at first (with a time constant about 1.6s), but at low speed the speed changes faster (as if the time constant dropped to about 0.6s).
Note that the fan slows down much more gradually than it speeds up, which means that it is not a linear, time-invariant system. In a linear system, superimposing a step-up and a step-down would cancel, so the responses to the step up and step down should add to a constant value—the fan most definitely does not have that property.
I was curious whether the difference was just apparent for large steps, or also for small ones, so I tried steps between PWM duty cycles of 100/256 and 160/256:

The small downward step is faster than before, though still substantially slower than the upward step of the same size, and with an initially slower response than the final convergence.
I’m going to try writing a couple of ad hoc controllers for the fan, to see if they behave better than the PID controller I’ve been using: open-loop control using just PWM=(setpoint-740)/25; a simple on/off control with a single threshold; hysteresis, using two thresholds instead of 1; PI control with no anti-windup; and a controller that goes to full on or full off when the error is large, to make a quick transition, switching to approximately the right PWM value, when the error is small, with PI control thereafter.
I think that the open-loop controller will have a steady, but wrong speed; the crude on/off controllers will make an audible pulsing of the fan motor; the PI controller will suffer from overshoot when making big steps, and the on/off/PI controller should make nice steps, if I can tune it right.
I implemented all the controllers and ran a test switching between setpoints of 1000RPM and 5000RPM every 30 seconds. Here are plots of the behavior with different control algorithms:

The PWM values computed by the various control algorithms show the integrator windup problem for PI clearly after the downward transitions—PI takes a long time to recover from the errors during the downward edge.

The mixed algorithm does a very good job of control, with little overshoot. The simple PI algorithm has substantial overshoot, particularly when the control loop wants a PWM value outside the range [0,255]. Open loop has significant offset and wanders a bit. On/off control oscillates at about 10hz, and adding hysteresis makes the oscillation larger but slower (about 5Hz).
Continuing the saga of the incubator project in the recent posts:
On my to-do list for the project
I got this done today, by drilling a hole in the box and soldering long wires onto the resistor and the thermistor, so that all the active electronics could live outside the box. Incidentally, “drilling” did mean using a drill bit, but I held it and turned it with my fingers—styrofoam is so soft and grainy that I feared a power drill would tear out big chunks.

Here is the interior of the styrofoam box, with the lid open. The 6″×12″ aluminum plate covers the bottom. The thermistor is on the left, propped up by a rubber foot, the resistor in is the center, and the fan is sitting on a foam pad on the right. (The foam is to reduce noise until I can get the fan proper mounted in a baffle.)
As expected, I can heat up the thermistor fairly quickly, but if I overshoot on the temperature, it takes a very long time for the closed box to cool back down. Cooling off just 1°C took over half an hour.
I did this also. With the box closed, the thermistor reading is fairly stable, with fluctuations of less than 0.1°C (which was the resolution with a single thermistor reading before adding 4 successive reads).
I fixed this also, using two techniques:
I think that changing which edge I used made a bigger difference than trying to suppress the erroneous reads digitally. I no longer hear the occasional hiccup where the control algorithm tries desperately to double or half the fan speed because of a misread timing pulse.
I changed from using conditional integration and back calculation of the integration error to using a decay of the integration error based on the difference between the computed PWM setting and the limit when the limits were exceeded. I’m not sure this improved anything though, and it introduces yet another parameter to tune, so I may go back to the previous method. I did play around with the tuning parameters for the fan loop today, and realized that I still don’t have good intuition about the effect of parameter changes. I noticed that the fan control was oscillating a little (small fluctuations around the desired speed, but big enough that I could hear the changes), and I found ways to reduce the oscillations, but at the expense of slower response to step changes.
I still need to do more thinking about the thermal modeling, since it is clear that I can’t afford overshoot when heating (though overshoot during slow cooling is unlikely to be a problem).
Still on my list with no progress:
I want to add to the list today:
Continuing the saga of the incubator project in the recent posts:
On my to-do list for the project
I got this done today, by drilling a hole in the box and soldering long wires onto the resistor and the thermistor, so that all the active electronics could live outside the box. Incidentally, “drilling” did mean using a drill bit, but I held it and turned it with my fingers—styrofoam is so soft and grainy that I feared a power drill would tear out big chunks.

Here is the interior of the styrofoam box, with the lid open. The 6″×12″ aluminum plate covers the bottom. The thermistor is on the left, propped up by a rubber foot, the resistor in is the center, and the fan is sitting on a foam pad on the right. (The foam is to reduce noise until I can get the fan proper mounted in a baffle.)
As expected, I can heat up the thermistor fairly quickly, but if I overshoot on the temperature, it takes a very long time for the closed box to cool back down. Cooling off just 1°C took over half an hour.
I did this also. With the box closed, the thermistor reading is fairly stable, with fluctuations of less than 0.1°C (which was the resolution with a single thermistor reading before adding 4 successive reads).
I fixed this also, using two techniques:
I think that changing which edge I used made a bigger difference than trying to suppress the erroneous reads digitally. I no longer hear the occasional hiccup where the control algorithm tries desperately to double or half the fan speed because of a misread timing pulse.
I changed from using conditional integration and back calculation of the integration error to using a decay of the integration error based on the difference between the computed PWM setting and the limit when the limits were exceeded. I’m not sure this improved anything though, and it introduces yet another parameter to tune, so I may go back to the previous method. I did play around with the tuning parameters for the fan loop today, and realized that I still don’t have good intuition about the effect of parameter changes. I noticed that the fan control was oscillating a little (small fluctuations around the desired speed, but big enough that I could hear the changes), and I found ways to reduce the oscillations, but at the expense of slower response to step changes.
I still need to do more thinking about the thermal modeling, since it is clear that I can’t afford overshoot when heating (though overshoot during slow cooling is unlikely to be a problem).
Still on my list with no progress:
I want to add to the list today: